HARESH LALVANI 2013-2014

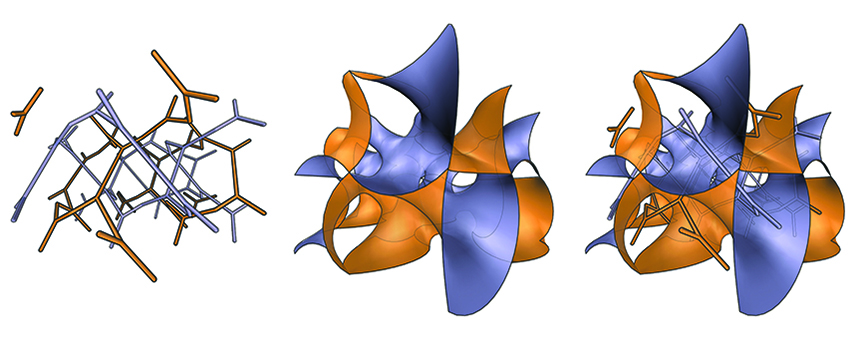
COMPLEMENTARY NETWORKS AND SURFACES

2013-2014

HARESH LALVANI

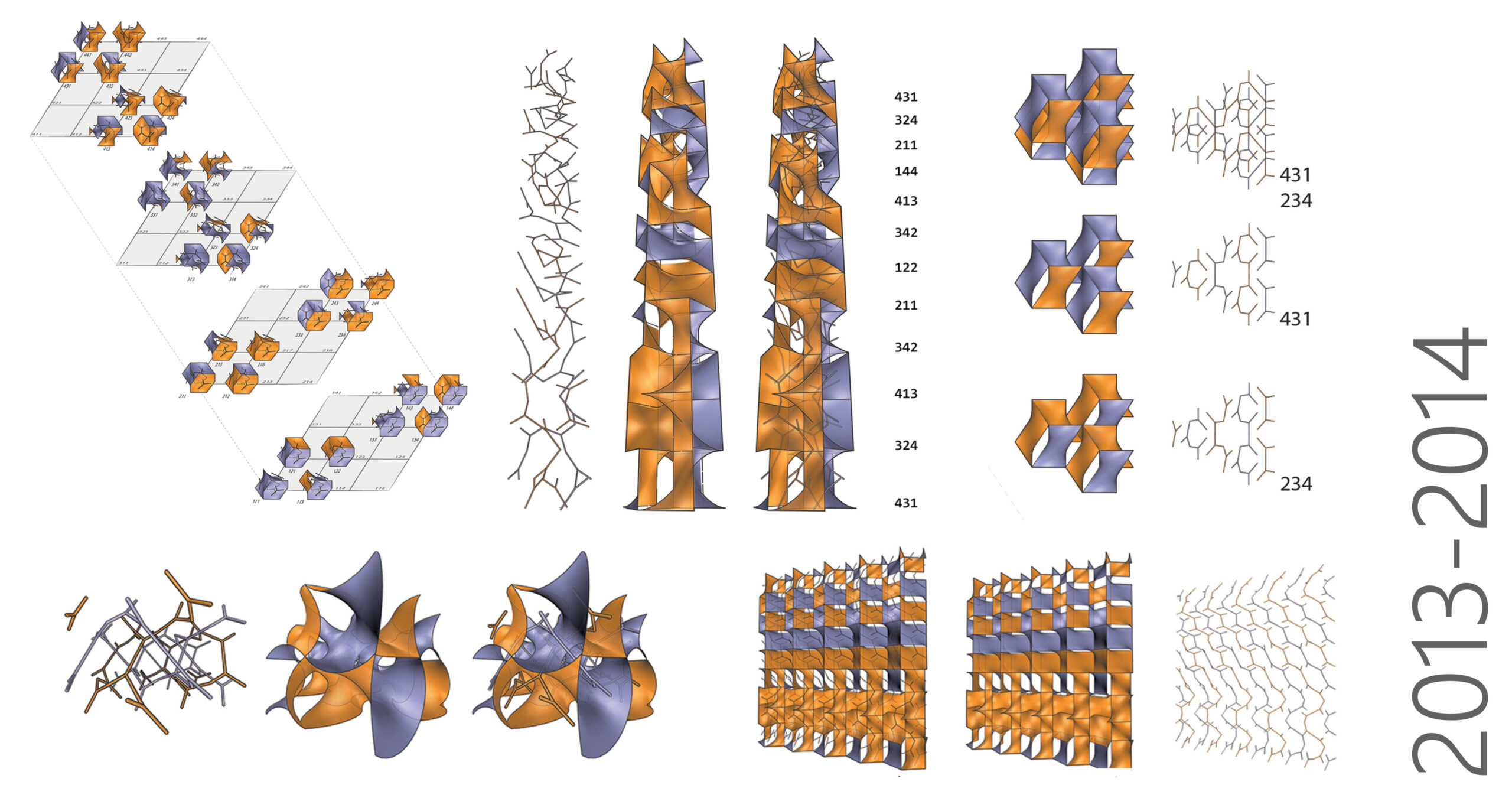
We present a space-building system comprising 2 pairs of complementary atomic modules, numbered 1 and 4, and 2 and 3 (bottom left, left page) that can generate endless spatial configurations based on any sequences of four numbers, 1,2,3 and 4, using only one matching rule. The four atoms can make “molecules”, “macro-molecules”, and larger composite surfaces using this rule and all can be number-coded. Spatial possibilities include closed 3-dimensional islands, pinched spaces that kiss at points or lines, or continuous spaces of different types, towers, mono-layers, multi-layers, protein-like configurations, etc. – all with the remarkable property that all generated surfaces always divide any space by a pair complementary networks. 

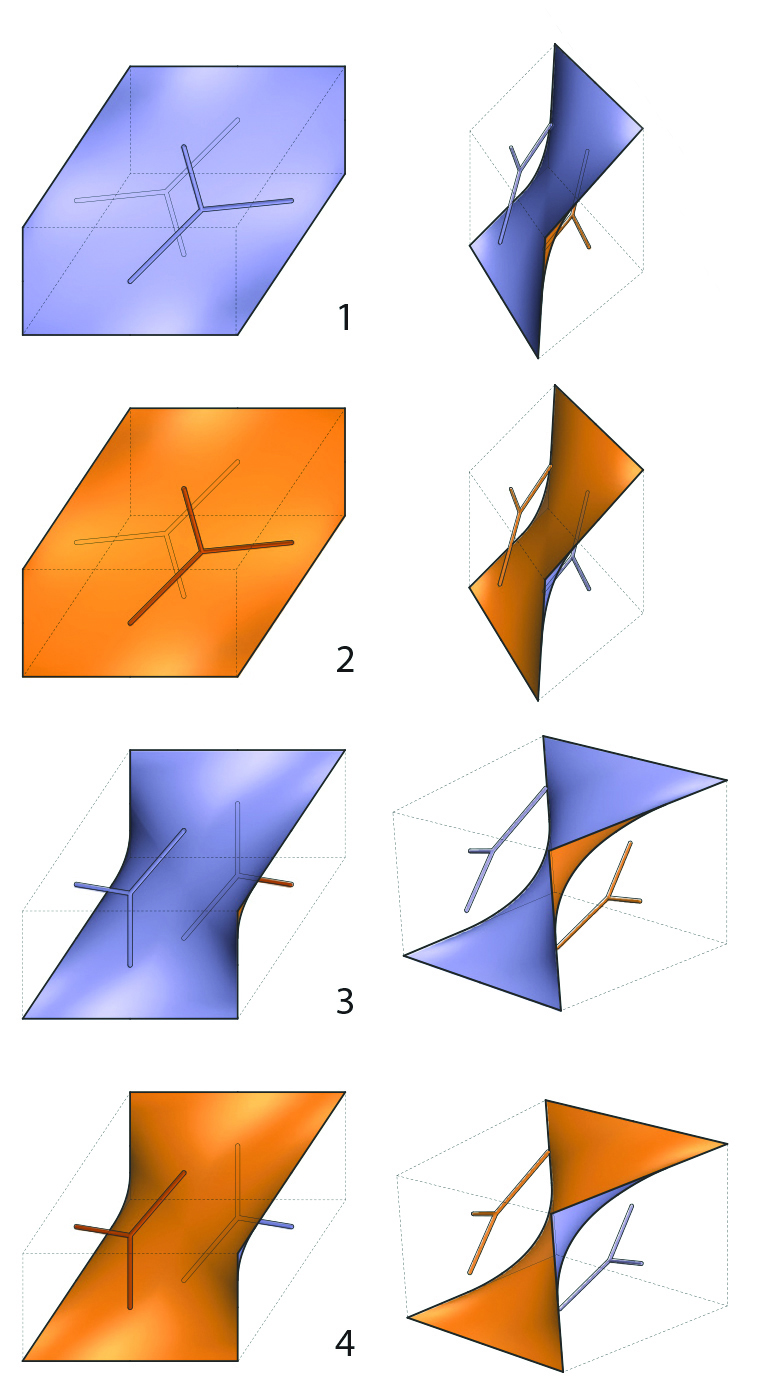
Each of the four modules is a 2-sided surface, a saddle hexagon, blue on one side and orange on the other. Each surface separates 2 complementary 3-pronged elements, also blue and orange to match the colors surface modules. The matching rule for populating space: prongs of same color must join.

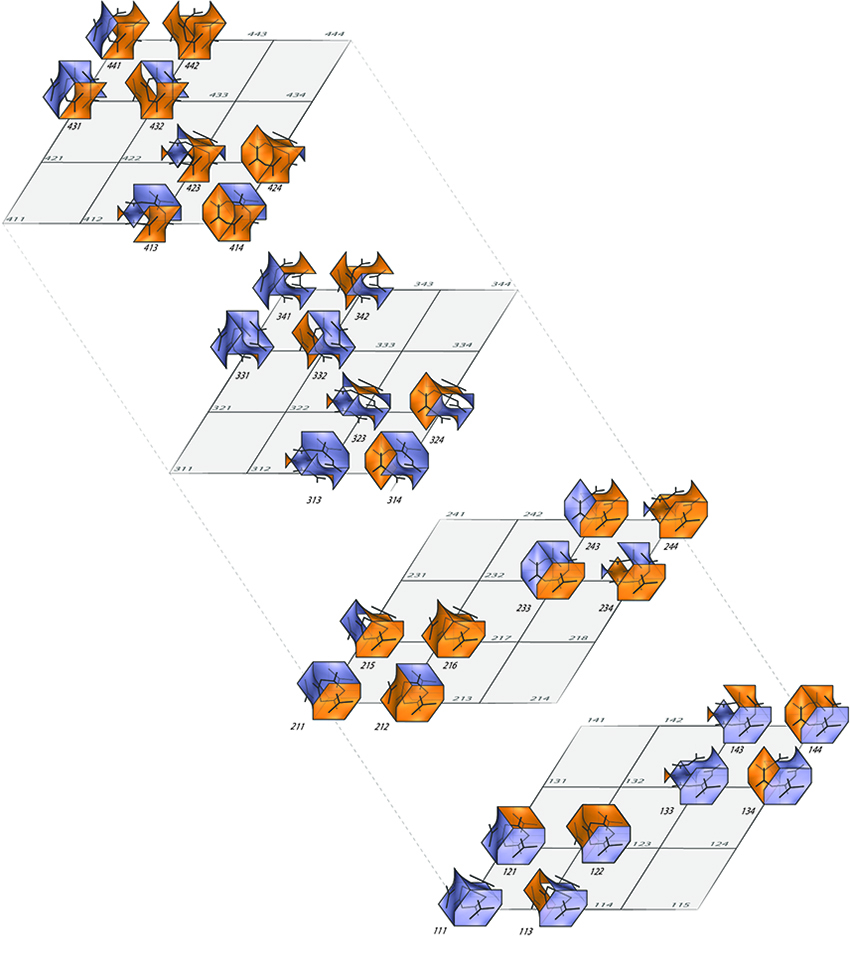
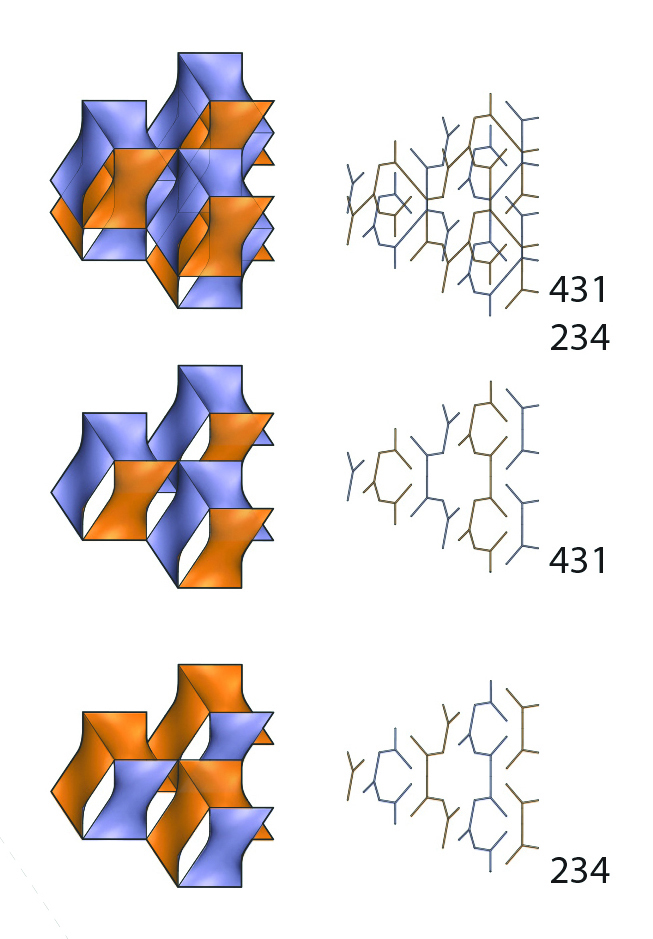
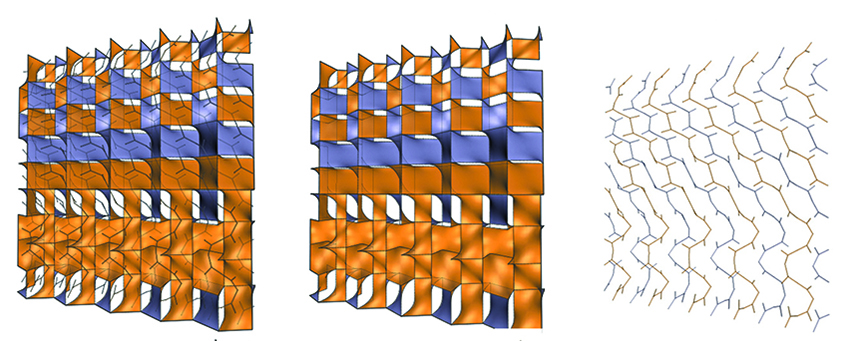
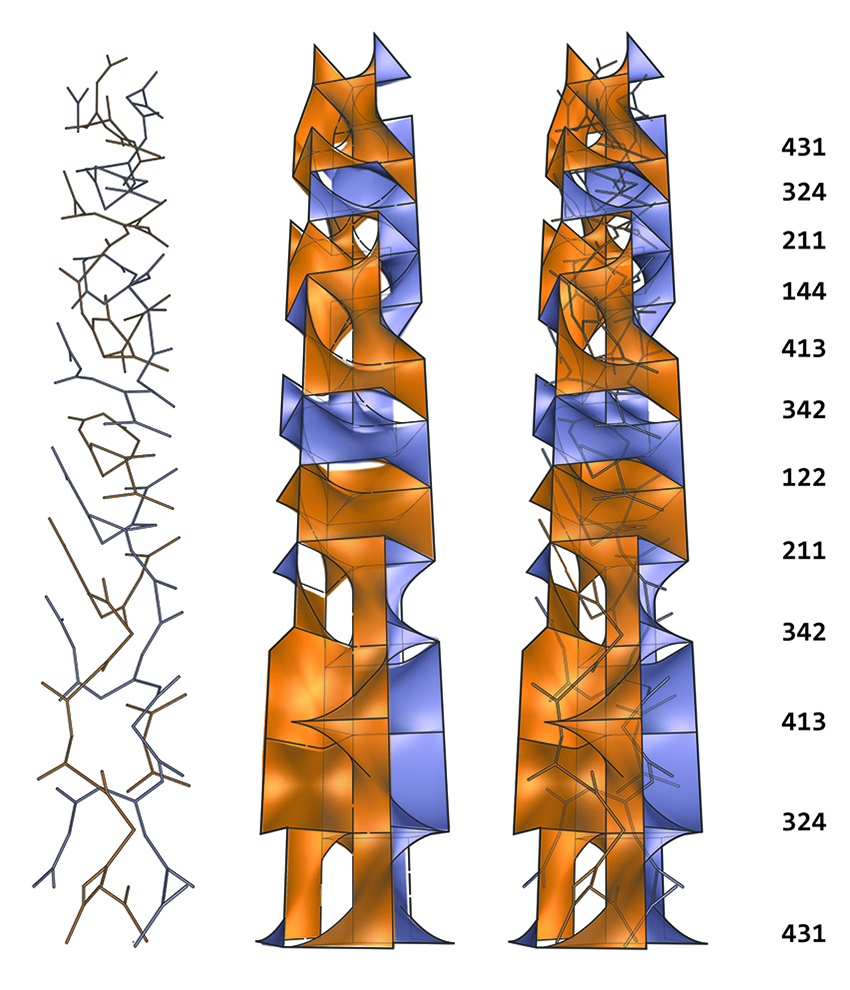
Single modules can be combined systematically to make clusters. As one example, the diagram (middle, left page) shows the generation of the 32 permissible combinations of a three-module cluster. Each cluster has a triplet number code which refers to the cyclic sequence of the base modules starting from the bottom and going counter-clockwise. The images on the upper right on left page show portions of a layered configuration and a possible building façade which is number-coded. The images on the right page shows curved variants of the system that preserve topology yet are different formal compositions.

The system shown here is one example of an infinite class of such systems based on the morphologic theory of tiling. Seen in the plan view, the system shown here corresponds to the n=3 tiling, where all edges (in plan) are parallel to 3 independent directions. This is one special case of tilings with n independent directions. Seen this way, Alan Schoen’s well-known gyroid corresponds to a curved variant of the n=2 case. This generalizes the 3-number code in the diagram on left page to a n-number code. By analogy, the triplet codons (3-base codons) of the DNA base sequences extend to n-base codons which may enable new biologies comprising genomes that are read n-bases at a time. Such transcription, even if denied in biology, would be possible with the morphological genome at different scales of magnitude from pecto-technology to architecture and beyond.

Computer Modeling: Lalvani Studio

Rendering: Ardon Lee